AbstractsEstimated margin data for Boosting and SVMFlorence d'Alche-Buc, Laboratoire d'Informatique de Paris 6, Paris In large margin algorithms such as boosting and SVM, training data that lie close to decision frontiers play a crucial role. We estimate the distribution of these “margin” training patterns and empirically investigate how to use it to cope with large data sets in boosting and SV machines. We principally focus on the understanding of boosting and then give some first results about SV machines. First we show that the estimated distribution of margin training data can be injected as initial distribution to be learnt in boosting algorithm. This considerably reduces complexity maintaining the high level of performance. Second, while using boosting, it appears as an empirical evidence that both first and last computed experts play a crucial role. The first expert is specialized on the easy-to-learn data provided a global trend for the decision. The second expert appears to be specialized in hard-to-learn data providing a local detailed decision. Thus a possible way to simplify boosting for large data sets consists in combining two hypothesis, one trained on the hard-to-learn training data and the other trained on the easy-to-learn training data. Of course, these two classifiers must have sufficient capacity to solve the two problems. This is the case for large enough MLPs. The application of this new method on several data sets illustrates its relevance. Finally, since most of hard-to-learn data lie in the margins of the classifiers, the estimation of this distribution can be used to provide a set of candidates support vectors. This set can be efficiently used to initialize a SVM algorithm implementation. Joint work with M.-R. Amini, Laboratoire d'Informatique de Paris 6, Paris, and Stephane Canu, PSI, INSA de Rouen, Mont Saint-Aignant. Error Estimates for Large Margin ClassifiersPeter Bartlett, Austrailan National University, Department of Systems Engineering We give upper and lower bounds on misclassification probability for large margin classifiers. For any class of thresholded real-valued functions satisfying a mild uniformity condition, achieving misclassification probability nearly as small as that of the best large margin classifier in the class requires an amount of data that grows with the logarithm of a certain covering number of the class. We present a number of applications of these results. Nearest neighbour classification and large margins Jonathan Baxter, Austrailan National University, Department of Systems Engineering Nearest neighbour methods are among the simplest and most widely used pattern classification techniques. Recent analysis has shown that the generalisation performance of classifiers optained by thresholding real-valued functions is intimately connected with the size of the “margins” of the training examples. In this talk I will present some experiments with a character classification problem showing that nearest neighbour algorithms also exhibit an association between the “margin” and the generalisation error. Some of the theory relevant to analysing this phenomenon will be discussed. Enlarging the Margins in Perceptron Decision TreesKristin Bennett, Mathematical Sciences Department, Rensselaer Polytechnic Institute Capacity control in Perceptron Decision Trees is typically performed by controlling their size. We have proven that other quantities can be as relevant to reduce their flexibility and combat overfitting. In particular, we derived an upper bound on the generalization error which depends both on the size of the tree and on the margin of the decision nodes. We now examine how these theoretical results can be incorporated into practical algorithms. We study three possible approaches all using the perceptron decision tree algorithm, OC1, as a baseline. OC1 is a top-down decision tree algorithm that optimizes each linear decision using a randomized search. The first algorithm, FAT, starts with the tree constructed by OC1 and constructs the tree with the hyperplanes of each OC1 node replaced by the maximum margin hyperplane implementing the same decision. The second approach, Margin OC1 (MOC1), alters the OC1 splitting criterion to minimize the original OC1 splitting criterion and maximize the decision margin at each node. Both FAT and MOC1 are hard margin approaches. The margin is the distance between the two closest points on either side of the decision hyperplane. The final algorithm utilizes soft margins in much the same manner as Support Vector Machines. In order to achieve larger margins, points are allowed to fall within the margin. The splitting criterion is modified to only count the points falling outside the margin as being correctly split. An extensive experimental study on real world data confirms our approach. Individually the margin-based approaches compared favorably to the unaltered OC1 algorithm. Each algorithm performs better or at least not significantly worse then OC1 on almost every dataset. OC1 did significantly worse than the best margin-based method on every dataset except one. Joint work with Nello Cristianini, Dept. of Engineering Mathematics,University of Bristol, John Shawe-Taylor, Dept. of Computer Science, Royal Holloway, University of London, and Donghui Wu, Department of Mathematical Sciences, Rensselaer Polytechnic Institute Are margins relevant in voting?Leo Breiman, Dept. of Statistics, Stanford University, First, I'll present evidence that in the case of arcing classifiers, higher margins do not imply lower generalization error. Then, I'll present a new combination method called half&half bagging which gets results competitive with Adaboost, but is of an entirely different type. Looking at half&half bagging, one can see more tranparently what is going on. The successful combination methods seem to be trying to find the analogue of the support vectors and fasten the boundary to these. It is not at all clear what the relevance of the margins is. Empirical Risk Approximation for Unsupervised Learning Joachim Buhmann, University of Bonn Unsupervised learning algorithms are designed to extract structure from data without reference to explicit teacher information. The quality of the learned structure is determined by a cost function which guides the learning process. This paper proposes EMPIRICAL RISK APPROXIMATION as a new induction principle for unsupervised learning. The complexity of the unsupervised learning models are automatically controlled by large deviation bounds. The maximal entropy principle with deterministic annealing as an efficient search strategy arises from the EMPIRICAL RISK APPROXIMATION principle as the optimal inference strategy for large learning problems. Parameter selection of learnable data structures is demonstrated for the case of K-means and distributional clustering. Discriminative Gaussian Mixture ModelsChris Burges, Lucent, Bell Laboratories Gaussian mixture models are commonly used for the speaker identification task. A model, or set of models, is built for each speaker, and maximum likelihood used to identify the speaker given the data. This method is not inherently discriminative: a model for a given speaker is built using data from only that speaker. In this talk I will discuss one method for adding discrimination to Gaussian mixture models using support vector machines, and give results on a NIST speaker identification task. Margin Distribution Bounds on GeneralizationNello Cristianini, University of Bristol A number of results have bounded generalization of a classifier in terms of its margin on the training points. There has been some debate about whether the minimum margin is the best measure of the distribution of training set margin values with which to estimate the generalization. Freund and Schapire and Shapire, COLT98 have shown how a different function of the margin distribution can be used to bound the number of mistakes of an on-line learning algorithm for a perceptron, as well as an expected error bound. We show that a slight generalization of their construction can be used to give a new pac style bound on the tail of the distribution of the generalization errors that arise from a given sample size. Our bound involves the sum of the squares of the distances by which points fail to meet a specified margin. For the maximal margin this sum is zero and the bound reduces to the standard one. For larger margins or classifiers that have training errors the bounds can be significantly better than previous ones. The analysis also suggests a different criterion to optimise when training a linear classifier. We present a polynomial algorithm for a modified Kernel based linear machine which directly minimizes this criterion. This algorithm handles training errors optimally with respect to the computed generalization error bound in contrast to previous approaches to handling errors which are heuristic. COLT98 Yoav Freund and Robert E. Schapire, Large Margin Classification Using the Perceptron Algorithm, Proceedings of the Eleventh Annual Conference on Computational Learning Theory, 1998. Joint work with John Shawe-Taylor, Dept. of Computer Science, Royal Holloway, University of London Large Margin Classification Using the Perceptron AlgorithmYoav Freund, AT&T Research We introduce and analyze a new algorithm for linear classification which combines Rosenblatt's perceptron algorithm with Helmbold and Warmuth's leave-one-out method. Like Vapnik's maximal-margin classifier, our algorithm takes advantage of data that are linearly separable with large margins. Compared to Vapnik's algorithm, however, ours is much simpler to implement, and much more efficient in terms of computation time. We also show that our algorithm can be efficiently used in very high dimensional spaces using kernel functions. We performed some experiments using our algorithm, and some variants of it, for classifying images of handwritten digits. The performance of our algorithm is close to, but not as good as, the performance of maximal-margin classifiers on the same problem. Joint work with Robert E. Schapire, AT&T Research Support Vector Neural NetworksThilo Friess, GMD FIRST, Berlin and University of Sheffield The kernel Adatron with bias and soft margin (KAb) is a new neural network alternative to support vector (SV) machines. It can learn large-margin decision functions in kernel feature spaces in an iterative “on-line” fashion which are similar to support vector machines. In contrast support vector learning is batch learning and is strongly based on solving constrained quadratic programming problems. Quadratic programming is nontrivial to implement and can be subject to stability problems. The kernel Adatron algorithm (KA) has been introduced recently. So far it has been assumed that the bias parameter of the plane in feature space is always zero, and that all patterns can be correctly classified by the learning machine. These assumptions cannot always be made. The kernel Adatron with bias and soft margin (KAb) combines the speed and simplicity of a neural network with the predictive power of SV machines. However the KAb does not, unlike to SV machines, suffer from any problems related to quadratic programming, and unlike to conventional neural networks the KAb's cost function is always convex such that it is guraenteed that the global optimum of the cost function will be found during the learning process. The kernel Adatron with bias and soft margin is introduced and discussed, then experimental studies using benchmarks and real data are presented which allow to compare the performance of kernel Adatrons and SV machines. A note on a scale-sensitive dimension of linear bounded functionals in Banach spacesLeonid Gurvits, NEC Research We show that 'B is of type p > 1’ is a necessary and sufficient condition for learnability of a class of linear bounded functionals with norm <= 1 restricted to the unit ball in Banach Space B. On the way we give a very short probabilistic proof for Vapnik's result (Hilbert Space and improved) and imrove our result with Pascal Koiran for convex hulls of indicator functions. The approach we use in this paper allows to connect various results about learnability and approximation. What linear discriminant techniques teach us about SVMsIsabelle Guyon, Clopinet Support Vector Machines were introduced and first applied to classification problems as alternatives to multi-layer neural networks. The high generalization ability provided by the Optimum Margin Classifier SVM, in particular, has inspired work on computational speedups as well as the fundamental theory of model complexity and generalization. At first glance, SVM classifiers appear to be nothing more than a generalized linear discriminant in a high-dimensional transformed feature space; indeed, many aspects of SVM classifiers can best be understood in relation to traditional linear discriminant techniques. However, SVM classifiers are more powerful than such traditional methods, in part because the natural way in which complexity can be adjusted in SVMs. The theory of SVMs sheds new light on the “curse of dimensionality,” in particular, the extent to which it is truly a “curse.” There are, moreover, relationships between the training algorithms of classical linear classifiers and those of SVMs that lead to new training methods for both types of classifier. Our presentation will include:
Joint work with David Stork, CRC, Ricoh Large Margin Rank Boundaries for Preference LearningRalf Herbrich, Dept. of Statistics, University of Technology Berlin In this talk we investigate the problem of learning a preference relation from a given set of ranked objects. The main difference between preference learning and standard classification learning is the demand, that the mapping from objects to ranks has to be transitive and asymmetric. To model this problem we present an approach that performs a linear mapping from objects to scalar utility values and thus guarantees transitivity and asymmetry. The learning of the preference between objects is formulated as a classification problem on pairs of objects and is solved by maximizing the margin at the rank boundaries defined on the utility function. The approach is extended to nonlinear utility functions by using the potential function method (the so called kernel trick), which allows to incorporate higher order correlations of features into the utility function at minimal computational costs. We will present some application in Information Retrieval tasks. Joint work with Thore Graepel, University of Technology Berlin Boosting RegressorsGrigoris Karakoulas, Global Analytics, CIBC There is growing interest in extending the boosting algorithm to regression problems. In this paper, we develop a boosting algorithm that incrementally builds a committee of independent “weak” regressors by dynamically adjusting the margin of the committee and finding the combining coefficients that minimize training error. The algorithm is compared against bagging and support vector regression machines on artificial and real-world datasets. Joint work with John Shawe-Taylor, Dept. of Computer Science, Royal Holloway, University of London Local training of Support Vector MachinesAdam Kowalczyk, Telstra Research Laboratories For a separable data set, a local learning rule (a modification of classical perceptron) will be presented. This modification of the classical perceptron generates a series of approximations of the ideal solution, with each update requiring a knowledge of a current approximation and of the tested training instance. The algorithm is proved to generate in Another, a soft margin algorithm designed to deal with a (linearly) non-separable data set, will also be discussed. It uses pairs of input points for updates of the hyperplane. In each iteration it decreases the primal (soft margin) cost function and it is able to iterate unless the desired solution (the global minimum) is reached. Joint work with Trevor Anderson, Telstra Research Laboratories Mathematical Programming in Machine LearningOlvi Mangasarian, Dept. of Computer Science, University of Madison, Wisconsin The role of mathematical programming in supervised and unsupervised machine learning will be outlined. Beginning with some early work, where linear programming was used to generate large margin linear and nonlinear classifiers, to more recent linear programming approaches to massive data discrimination via support vector machines, the role of mathematical programming will be highlighted. Other problems addressed as concave function minimization on a polytope include: feature selection, k-median clustering and parsimonious least-norm approximation. Theoretical results justifying these approaches will be presented together with computational results on publicly available data sets.
|
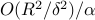 iterations a hyperplane separating a finite subset of a Euclidean space with a margin larger than
iterations a hyperplane separating a finite subset of a Euclidean space with a margin larger than 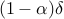 , where
, where 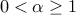 and
and 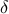 is the maximal margin.
is the maximal margin. -AdaBoost Classification
-AdaBoost Classification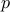 -norm Perceptron and normalized Winnow algorithm.
-norm Perceptron and normalized Winnow algorithm.