|
Summaries
V. Vapnik (AT&T Research):
The SVM method for function approximation (Theory):
Will get better SVM performance if find kernels that minimize D/r,
where D is diameter of minimal sphere containing data in hi-dim space, and r
is the margin
“Transductive inference” (train on all possible labelings of the test set,
choose min. D/r) should also help performance
Can get conditional probabilities out of SVMs by solving 1-dim integral
equation.
G. Wahba (U. Wisconsin at Madison):
Reproducing kernel spaces, smoothing spline ANOVA spaces, SV machines, and all
that (Theory):
There is a 1-1 correspondence between reproducing kernel hilbert spaces
(RKHS), and positive definite functions; and between positive definite
functions, and zero-mean Gaussian stochastic processes.
Replacing the logit cost functional, in penalized log-likelihood methods,
gives several SVMs - hence there is relation between old techniques and SVMs
(this was a recurring theme).
For classification, replacing the logit likelihood functional by SVM
functional is a natural way to concentrate on estimating logit near the
classification boundary.
L. Kaufman (Bell Labs, Lucent):
Solving the QP problem arising in SV classification (Applications):
For SVM training, there are methods for computing only that part of the
hessian that you need. The idea is to solve a sequence of equality constrained
problems. Can project variables into a subspace in two interesting ways:
such that the resulting hessian's inverse can be computed very efficiently;
this requires more storage;
such that hessian itself is not needed - can
compute gradient very efficiently; needs lees storage, more compute power.
C. Burges (Bell Labs, Lucent):
The Geometry of support vector machines (Theory):
The SVM mapping induces a natural Riemannian metric on the data
The kernel contains more information than the corresponding metric
This observation gives useful tests for positivity of any proposed SVM
kernel
B. Scholkopf (Max Planck at Tuebingen, GMD):
Kernel principal component analysis (Theory + Applications):
Can use the kernel mapping trick for any algorithm that depends only on dot
products of the data: can apply this observation to construct a nonlinear
version of PCA
Y. Freund (AT&T Research):
AdaBoost as a procedure for margin maximization (Theory + Applications):
Naturally occurring norms in AdaBoost (the best-performing boosting
algorithm known to date) are 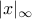 and and 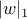 (x is data, w margin
vector); for SVMs they are (x is data, w margin
vector); for SVMs they are 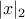 , , 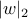 . .
Corresponding bounds imply that AdaBoost will beat SVMs when most features
are irrelevant, and vice versa.
K. Mueller (GMD FIRST, Berlin):
Predicting Time Series with SVMs (Applications):
SVMs give better regression results than other systems on noisy data. In
particular, they give equal or better performance than RBFs (despite fixed
widths) on Mackey-Glass times series, and much better performance (29%) than all
other published results on the Sante Fe time series competition, data set “D”.
SVM classification is currently the best in the world for charmed quark detection.
T. Joachims (U. Dortmund):
SV machines for text categorization (Applications):
SVMs give much better results, and are much more robust, than other methods
tried, for a text categorization problem.
F. Girosi (CBCL, MIT):
SVMs, regularization theory, and sparse approximation (Theory):
A modified version of the Bais Pursuit De-Noising algorithm is equivalent
to an SVM. RKHS play a fundamental role in SVMs.
K. Bennett (Rensselaer Polytechnic Institute):
Combining SV methods and mathematical programming methods for induction
MPM has a rich history: MPM and SVM use same canonical form, and are easily
combined
MP could itself benefit from learning theory
M. Stitson (Royal Holloway London):
SV ANOVA decomposition (Theory + Applications)
ANOVA decomposition splines kernels give better results than regular
splines and polynomial kernels on the Boston Housing regression problem.
J. Weston (Royal Holloway London):
Density estimation using SV machines (Theory)
Can modify the SVM algorithm to estimate a density (differences:
this results in LP problem, and kernels are not Mercer kernels)
Showed a natural way to use kernels of different widths.
A. Smola (GMD FIRST, Berlin):
General cost functions for SV regression (Theory)
By using path following interior point methods for SVM training, can extend
class of cost functions
This is useful because should match cost function to noise, where possible,
for best performance.
J. Shawe-Taylor (Royal Holloway London):
Data-sensitive PAC analysis for SV and other machines (Theory)
PAC bounds can be used to put SRM on a rigorous, data-dependent footing for
SV machines.
N. Christianini (U. Bristol):
Bayesian voting schemes and large margin algorithms (Theory)
Bayesian learning algorithms can be regarded as large margin hyperplane
algorithms in high dimensional feature space, where the margin depends on the
prior.
D. Schuurmans (U. Pennsylvania & NEC Research):
Improving and generalizing the basic maximum margin algorithm (Theory)
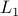 (as opposed to (as opposed to 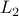 ) margins will be a win if target vector is sparse,
e.g. text classification. ) margins will be a win if target vector is sparse,
e.g. text classification.
Can use unlabeled data, which gives metric on hypothesis space, to improve
generalization performance.
|
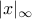 and
and 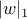 (x is data, w margin
vector); for SVMs they are
(x is data, w margin
vector); for SVMs they are 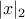 ,
, 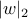 .
.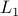 (as opposed to
(as opposed to 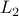 ) margins will be a win if target vector is sparse,
e.g. text classification.
) margins will be a win if target vector is sparse,
e.g. text classification.