ScheduleMorning SessionChair: Chris Williams and Carl Rasmussen
Afternoon SessionChair: Alex Smola, Roderick Murray Smith
AbstractsOptimality Conditions for SVM algorithmsChris Charalambous, Public and Business Administration, University of Cyprus The purpose of this paper is to provide an in depth analysis of the basic ideas behind Support Vector Machines. Although the subject can be said to have started in late seventies (Vapnik, 1979), it is only now receiving increasing attention. The method has been applied with great success in areas such as handwritten digit recognition, speaker identification and face detection in images. In this paper some new results will be presented. We will show under what conditions the primal and the dual solutions are unique. Furthermore, a pathological case neglected by the previous researchers will be presented and analyzed. Online Gaussian Process ClassifiersLehel Csato, NCRG Aston Abstract (PS) Joint work with Manfred Opper, NCRG Aston A PAC–Bayesian Bound for Linear SVMsRalf Herbrich, TU Berlin, Department of Computer Science We present a new bound on the generalisation error of linear SVM classifiers which is by magnitudes tighter than previous margin bounds and gives non-trivial results in parameter regimes relevant to real world problems. The new bound is inherently connected to the luckiness approach of Shawe-Taylor et.al. (1996) by using a sample-based complexity measure: the volume of a subset of version space relative to the volume of parameter space. For SVMs such a quantity is given by the margin which characterises the volume of the largest ball that fits into version space. The improvement over previous bounds can be explained by a fundamentally different reasoning. While standard VC theory treats each classifier separately and aims at bounding its generalisation error, the PAC-Bayesian framework (McAllester, 1998) considers subsets of the model space and bounds the average generalisation error over the subset. These bounds involve the Bayesian prior probability of the subset of classifiers. In constrast to standard Bayesian performance guarantees the PAC-Bayesian results do not need to assume a correctly specified prior. In order to apply these bounds to single classifiers it is necessary to identify a subvolume of version space such that its average generalisation error is strictly related to the generalisation error of the single classifier. We show that the generalisation error of the SVM classifier is bounded from above by twice the average generalisation error of the subset of all classifiers contained in the ball around it. This relation makes it possible to apply the PAC-Bayesian result to SVM classifiers and leads to the new bound. Joint work with Thore Graepel, TU Berlin Mixtures of Gaussian Process Priors: Applications in Regression, Density Estimation, Classification, and Inverse Quantum Statistics.Jörg Lemm, Physik Department, Universität Münster Mixtures of Gaussian process priors generalising the Gaussian process approach provide a flexible method to model complex prior densities. In contrast to parametric approaches like neural networks the implementation of a priori information can be explicitly in terms of the function of interest. In contrast to Gaussian processes prior densities are not restricted to be concave. The contribution will focus on recent applications of mixtures of Gaussian processes to image completion (regression) and Inverse Quantum Statistics (reconstruction of potentials from data). How to Adapt SVM in Order to Classifiy Natural Language Text?Edda Leopold, GMD Bonn The rank-frequency distribution of lexical units in natural language texts has special characteristcs. It is extreemely skewed, and can be discribed by a displaced hyperbolic function (Zipfian law). Furthermore: as a thumb rule 50% of the types of a text of any length occures only once due to the productivity of morphosyntactic rules. My talk will outline the characteristics of word-frequency. distributions. I shall propose kernel functions appropriate to linguistic data and shall ask how to cope with a potentially infinte dimensional sample space. Gaussain Processes in Dynamic Systems ApplicationsRoderick Murray-Smith, Department of Computing Science, Glasgow University Learning curves for GP and SVM, some good approximationsManfred Opper, NCRG Aston Recently, Peter Sollich 1 has produced a nice approximative method to calculate learning curves for GP regression. Unfortunately, based on exact expressions for the Bayesian generalization error that can be derived in that case, the method did not seem to be extendable to nonGaussian likelihoods and other models like SVM. I will use an entirely different approach based on partition functions together with a central limit + Laplace approximation to rederive his result for regression and extend it to other types of models like GP and SVM classifiers. I will also discuss the limits where the theory becomes exact/or a bad approximation. Introduction to Gaussian Process Priors (Tutorial)Carl Edward Rasmussen, Institute of Mathematical Modelling, Technical University of Denmark Variational Bayesian Model Selection for SV ClassifiersMatthias Seeger, Artificial Intelligence, University of Edinburgh We present a variational Bayesian method for model selection over families of kernels classifiers like Support Vector machines or Gaussian processes. The algorithm needs no user interaction and is able to adapt a large number of kernel parameters to given data without having to sacrifice training cases for validation. This opens the possibility to use sophisticated families of kernels in situations where the small ‘‘standard kernel’’ classes are clearly inappropriate. We relate the method to other work done on Gaussian processes and clarify the relation between Support Vector machines and certain Gaussian process models. A PAC Style analysis of SV MachinesJohn Shawe-Taylor, Royal Holloway College, London Recent results linking pac analysis with Bayesian methods will be reviewed. In particular Bayesian evidence can be analysed within the pac framework and a relation developed between margin analysis and the posterior distribution. Introduction to Support Vector Machines (Tutorial)Alex J. Smola, GMD FIRST, Berlin After a brief overview over kernel methods and the setting of learning problems from the SV perspective, I'll focus on the choices that lead to quite different algorithmic results in Gaussian Processes and Support Vector Machines. These can be found mainly in the choice of the cost function where GP use additive Gaussian noise, whereas SVM obtain sparse solutions via the softmargin loss. The estimates are obtained by solving a convex optimization problems with (SVM) or without (GP) constraints. Further differences and relations regarding model selection will be pointed out. Probabilistic methods for Support Vector MachinesPeter Sollich, Mathematics, King's College London I describe a framework for interpreting Support Vector Machines (SVMs) as maximum a posteriori (MAP) solutions to inference problems with Gaussian Process priors. This can provide intuitive guidelines for choosing a ‘good’ SVM kernel. It can also assign (by evidence maximization) optimal values to parameters such as the noise level |
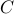which cannot be determined unambiguously from properties of the MAP solution alone (such as cross-validation error). I illustrate this using a simple approximate expression for the SVM evidence. Once