Disks are slow and RAM is fast. Everyone knows that. But many optimization algorithms don’t take advantage of this. More to the point, disks currently stream at about 100-200 MB/s, solid state drives stream at over 500 MB/s with 1000x lower latency than disks, and main memory reigns supreme at about 10-100 GB/s bandwidth (depending on how many memory banks you have). This means that it is 100 times more expensive to retrieve instances from disk rather than recycling them once they’re already in memory. CPU caches are faster yet with 100-1000 GB/s of bandwidth. Everyone knows this. If not, read Jeff Dean’s slides. Page 13 is pure gold.
Update (11/2022): some things have gotten a lot faster over the past decade. For instance, SSDs now regularly deliver multiple GB/s. The number of requests has increased dramaticaly, too, to several 100k IOPS (IO Operations Per Second). For a recent comparison check out this Anandtech benchmark. At the same time, memory bandwidth has increased to 100-1000 GB/s, depending on the system. Many variants of Jeff Dean’s latency numbers have sprung up. One of the more recent ones is the one by Colin Scott.
Ok, so what does this mean for machine learning? If you can keep things in memory, you can do things way faster. This is one of the key ideas behind Spark. It’s a wonderful alternative to Hadoop. In other words, if your data fits into memory, you’re safe and you can process data way faster. A lot of datasets that are considered big in academia fit this bill (in 2022 you can easily rent or buy 256-1024GB instances). But what about real big data? Essentially you have two options - have the systems designer do the hard work or change your algorithm. This post is about the latter. And yes, there’s a good case to be made about who should do the work: the machine learners or the folks designing the computational infrastructure (I think it’s both).
So here’s the problem: Many online algorithms load data from disk, stream it through memory as efficiently as possible and discard it after seeing it once, only to pick it up later for another pass through the data. That is, these algorithms are disk bound rather than CPU bound. Several solvers try to address this by making the disk representation more efficient, e.g. LibLinear or VowpalWabbit, both of which use their own internal representation for efficiency. While this still makes for quite efficient code that can stream up to 10-100TB of data per hour, in any given pass, main memory is still much faster. This has led to the misconception that many machine learning algorithms are disk bound. But, they aren’t …
What if we could re-use data that’s in memory? For instance, use a ringbuffer where the disk writes into it (much more slowly) and the CPU reads from it (100 times more rapidly). The problem is what to do with an observation that we’ve already processed. A naive strategy would be to pretend that it is a new instance, i.e. we could simply update on it more than once. But this is very messy since we need to keep track of how many times we’ve seen the instance before, and it creates nonstationarity in the training set.
A much cleaner strategy is to switch to dual variables, similar to the updates in the Dualon of Shalev-Shwartz and Singer. This is what Shin Matsushima did in our dual cached loops paper (the StreamSVM implementation unfortunately has fallen into disrepair in the past decade). Essentially, it keeps data in memory in a ringbuffer and updates the dual variables. This way, we’re guaranteed to make progress at each step, even if we’re revisiting the same observation more than once. To see what happens have a look at the graph below:
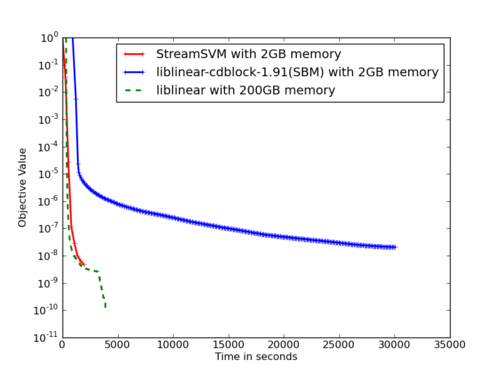
It’s just as fast as LibLinear provided that it’s all in memory. Algorithmically, what happens in the SVM case is that one updates the Lagrange multipliers αi, while simultaneously keeping an estimate of the parameter vector w available.
That said, this strategy is more general: reuse data several times for optimization while it is in memory. If possible, perform successive updates by changing variables of an optimization that is well-defined regardless of the order in which (and how frequently) data is seen.