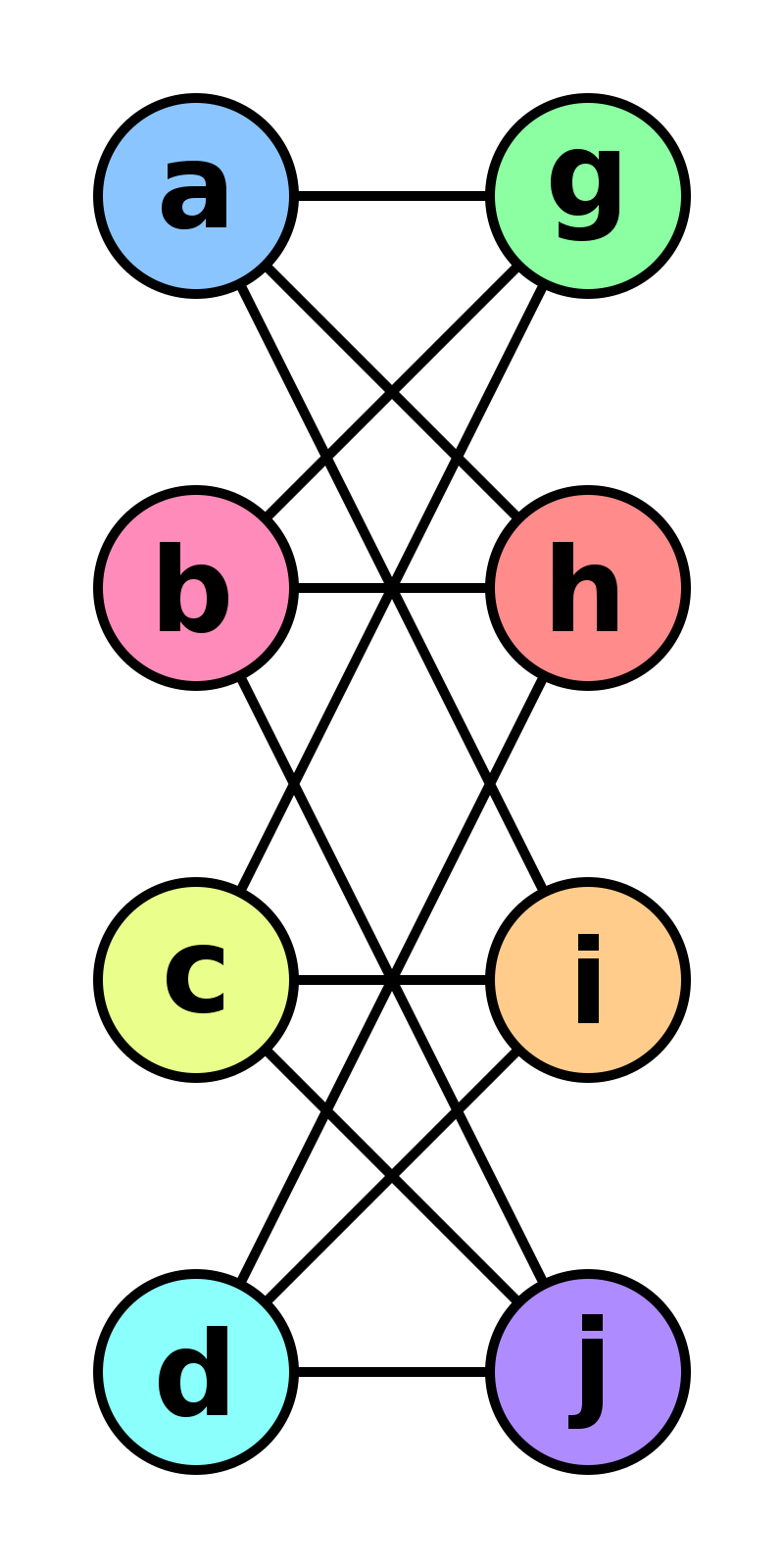
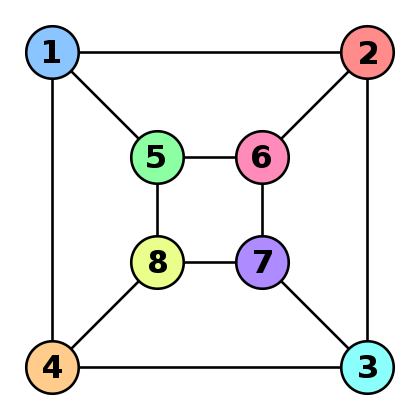
The Weisfeiler-Leman algorithm and estimation on graphs Imagine you have two graphs \(G\) and \(G′\) and you’d like to check how similar they are. If all vertices have unique attributes this is quite easy:
- forall vertices \(v \in G \cup G′\) do
- check that \(v \in G\) and that \(v \in G′\)
- check that the neighbors of \(v\) are the same in \(G\) and \(G′\)
This algorithm can be carried out in linear time in the size of the graph. Unfortunately, many graphs do not have vertex attributes, let alone unique vertex attributes. In fact, graph isomorphism, i.e. the task of checking whether two graphs are identical, is a hard problem (it is still an open research question how hard it really is). In this case the above algorithm cannot be used since we have no idea which vertices we should match up.
The Weisfeiler-Leman algorithm (see David Bieber’s blog post for a pretty visualization) is a mechanism for assigning fairly unique attributes efficiently. Note that it isn’t guaranteed to work, as discussed in this paper by Douglas in 2011. This would solve the graph isomorphism problem after all. The idea is to assign fingerprints to vertices and their neighborhoods repeatedly. We assume that vertices have an attribute to begin with. If they don’t then simply assign all of them the attribute 1. Each iteration proceeds as follows:
- forall vertices \(v \in G\) do
- compute a hash of \((a_v,a_{v_1}, \ldots a_{v_n})\) where \(a_{v_i}\) are the attributes of the neighbors of vertex \(v\).
- use the hash as vertex attribute for \(v\) in the next iteration.
The algorithm terminates when this iteration has converged in terms of unique assignments of hashes to vertices. Note that it is not guaranteed to work for all graphs. In particular, it fails for graphs with a high degree of symmetry, e.g. chains, complete graphs, tori and stars. However, whenever it converges to a unique vertex attribute assignment it provides a certificate for graph isomorphism. Moreover, the sets of vertex attributes can be used to show that two graphs are not isomorphic (it suffices to verify that the sets differ at any stage).
Shervashidze et al. 2012 use this idea to define a similarity measure between graphs. Basically the idea is that graphs are most similar if many of their vertex identifiers match since this implies that the associated subgraphs match. Formally they compute a kernel using
\[k(G,G′) = \sum_{i=1}^d \lambda_d \sum_{v \in V} \sum_{v' \in V'} \delta(a(v,i), a(v',i))\]
Here \(a(v,i)\) denote the vertex attribute of \(v\) after WL iteration \(i\). Morevoer, \(\lambda_d\) are nonnegative coefficients that weigh how much the similarity at level d matters. Rather than a brute-force computation of the above test for equality we can thus sort vertex attribute sets. Note that vertices that have different attributes at any given iteration will never have the same attribute thereafter. This means that we can compare the two sets at all depths at at most \(O(d \cdot (|V|+|V'|))\) cost.
A similar trick is possible if we want to regress between vertices on the same graph since we can use the set of attributes that a vertex obtains during the iterations as features. Finally, we can make our life even easier if we don’t compute kernels at all and use a linear classifier on the vertex attributes directly.