AbstractsCombining Support Vector and Mathematical Programming Models for InductionK. Bennett, Mathematical Sciences Department, Rensselaer Polytechnic Institute Research in mathematical programming (MP) has much to contribute to support vector machines (SVM) beyond powerful optimization algorithms. Existing MP approaches to modeling induction problems are closely related to SVM. In this talk we examine MP models for classification, regression, and clustering problems. We will show how SVM concepts are readily incorporated into these models. The result is improved performance of the MP models and suggestions for new research directions for SVM. Geometry of Support Vector MachinesC. Burges, Lucent, Bell Laboratories The kernel mapping inherent in support vector machines induces a metric on the space in which the data lives (“input space”). I show that this metric can be expressed in terms of the kernel; that every positive Riemannian metric on input space has an associated kernel mapping; and that positivity of the metric leads to some very simple conditions that the kernel must satisfy, which are much easier to check than Mercer's condition. I will also describe work to incorporate known invariances of the problems directly into the kernels themselves. Time permitting, I will also review some experimental results on using various bounds to determine optimal SVM parameter values. Bayesian voting schemes and large margin algorithmsNello Cristianini, University of Bristol It is often claimed that one of the main distinctive features of Bayesian Learning Algorithms is that they don't simply output one hypothesis, but rather an entire distribution of probability over an hypothesis set: the Bayes posterior. An alternative perspective is that they output a linear combination of classifiers, whose coefficients are given by Bayes theorem. Such a linear combination can be described like a hyperplane in a high dimensional space: a kind of hypothesis commonly used in Statistical Learning Theory. One of the concepts used to deal with thresholded convex combinations is the 'margin’ of the hyperplane with respect to the training sample, which is correlated to the predictive power of the hypothesis itself. In this work, we study the average margin of the Bayesian Classifiers in the case of pattern classification, with a uniform prior. We prove that under certain conditions it can be large. The average margin is conjectured to be a good indicator of the generalization power of the hypothesis, as suggested by experimental results and theoretical results on analogous quantities. Adaboost as a procedure for margin maximizationY. Freund, AT&T Labs - Research Adaboost (Freund, Schapire95) is an algorithm for improving the performance of learning algorithm. It does that by running the base learning algorithm several times and combining the resulting hypotheses by a weighted majority rule. It has recently been demonstrated that the majority rule has unexpectedly low generalization error (Cortes and Drucker 96, Breiman 96, Quinlan 96). It has also been shown, both theoretically and experimentally, that this behavior is connected to the fact that the weighted majority vote rule has large margins (Schapire, Freund, Bartlett, Lee 97). These results establish an interesting connection between Support Vector Machines and Adaboost. An interesting difference between the method is that in SVM one uses the Support Vector Machines, Regularization Theory and Sparse Approximation.F. Girosi, Center for Biological and Computational Learning, MIT In this talk I will discuss the equivalence between two different approximation techniques: the Support Vector Machine (SVM), proposed by V. Vapnik (1995), and a modified version of the Basis Pursuit De-Noising algorithm (BP) (Chen, 1995; Chen, Donoho and Saunders, 1995). BP is an instance of a sparse approximation technique, in which a function is reconstructed by using the least possible number of basis functions chosen from a large set (dictionary). We show that, under certain conditions, these two techniques are equivalent in the following sense: if applied to the same data set they give the same solution, which is obtained by solving the same quadratic programming problem. We also present a derivation of the SVM technique in the framework of regularization theory, rather than statistical learning theory, establishing a connection between SVM, sparse approximation and regularization theory. A preprint can be obtained here (AI Memo 1606). Support Vector Machines for Text CategorizationThorsten Joachims, Universitaet Dortmund This presentation explores the use of Support Vector Machines (SVMs) for learning text classifiers from examples. It identifies the particular properties of learning with text data: (a) very high dimensional (> 10000) input spaces, (b) most of the features are relevant (i.e. dense target concepts), and (c) sparse instance vectors. Theoretical considerations indicate that SVMs are well suited for learning in this setting. Empirical results support the theoretical findings. SVMs achieve substantial improvements over the currently best performing methods, eliminating the need for feature selection. Furthermore, their robustness makes them very promising for practical applications. SVMs behave consistently well over a variety of different text categorization tasks without any need for manual parameter tuning. Solving the Quadratic Programming problem arising in support vector classificationL. Kaufman, Lucent, Bell Laboratories The support vector technique suggested by Cortes and Vapnik is designed to solve the classification problem of determining the class of a data point when you are given some characteristics of the point( a vector ) and many “training” data of classes and characteristics. As shown by Cortes and Vapnik, the support vector technique leads to an indefinite quadratic programming problem with a dense and structured matrix, bound constraints, and one general equal- ity constraint. The number of rows in the matrix equals the number of training data points. Thus for a problem with thousands of training points, just computing the matrix for the quadratic programming problem is expensive and one may not be able to store it. In this paper we discuss several methods for solving the underlying quadratic programming problem including a projected Newton approach and a conju- gate gradient approach. We show how each can be implemented to take advantage of the nature of solution, the con- straints, and the matrix. Support Vector Machines for Dynamic Reconstruction of Chaotic ProcessesD. Mattera and S. Haykin, Neurocomputation for Signal Processing Group, McMaster University Dynamic reconstruction is an inverse problem that deals with recostucting the dynamics of an unkown system, given a noisy time series represeting the evoluion of one variable of the system with time. The solution to the problem rests on Takens’ embedding theorem. The reconstruction proceeds by using the time series to build a predictive model of the system and then using iterated predction to test what the model has learned from the training data on the dynamics of the system. The training is performed in an open loop mode of operation, whereas the test (i.e., generlaization) is performed in a closed loop mode of operation. This is indeed a difficult learning task. In this paper we present the results of an investigation into the use of the support vactor machine for solving the dynamic reconstruction problem. Two series of experiments are described, one using data from a noisy Lorenz attarctor, and the other using real life data on the radar backscatter from an ocea surface. Results on a comaprison with a regularized radial- basis function netwrok will also be presented. Predicting Time Series with Support Vector MachinesK.-R. Müller, GMD First, Berlin Support Vector Machines are used for time series prediction and compared to radial basis function networks. We make use of two different cost functions for Support Vectors: training with (i) an epsilon-insensitive loss and (ii) Huber's robust loss function and discuss how to choose the regularization parameters in these models. Two applications are considered: data from (a) a noisy (normal and uniform noise) Mackey Glass equation and (b) the Santa Fe competition (set D). In both cases Support Vector Machines show an excellent performance. In case (b) the Support Vector approach improves the best known result on the benchmark by a factor of 37%. Support Vectors in Natural Language Disambiguation TasksAmichay Oren and Dan Roth, University of Illinois - Urbana/Champaign Learning problems in the natural Language domain often map the text to a space whose dimensions are the measured features of the text, e.g., its words. Two characteristic properties of this domain are that its dimensionality is very high and that both the learned concepts and the instances reside very sparsely in the feature space. Naive statistical techniques usually address these problems by first reducing the dimensionality, possibly losing some of the information in the data. We will present the use of two techniques that seem to thrive in the presence of a large number of features: multiplicative-update learning algorithms and Support Vector Machines. We study the problem of Context-Sensitive Spelling Correction (This is the task of fixing spelling errors that happen to result in valid words, such as substituting to for too, casual for causal, and so on.). We adapt these algorithm to work in this domain and show that they are able to exploit the full set of features and outperform methods that first prune the feature space. We study issues that are related to adapting the algorithms to an unfamiliar test set in an on-line setting, and the significance of the support vectors in this domain. Kernel Principal Component AnalysisBernhard Schölkopf , MPI für biologische Kybernetik, Tübingen, and GMD Berlin A new method for performing a nonlinear form of Principal Component Analysis is proposed. By the use of SV kernel functions, one can efficiently compute principal components in high-dimensional feature spaces, related to input space by some nonlinear map; for instance the space of all possible d-pixel products in images. The algorithm consists of solving an Eigenvalue problem for the kernel dot product matrix. Improving and generalizing the basic maximum margin algorithmDale Schuurmans, U. Pennsylvania & NEC Research I consider a simple extension of Vapnik's maximum margin algorithm that exploits additional unlabeled training examples. The idea is to measure the distance between hyperplanes, not by the Data-sensitive PAC Analysis for SV and Other MachinesJohn Shawe-Taylor, Royal Holloway London Contrary to popular belief, to obtain rigorous PAC bounds for SV machines, it is not sufficient to estimate the VC dimension of large margin hyperplanes, since standard structural risk minimisation cannot be applied in this case. Resolving this technical difficulty requires a bound on covering numbers in terms of the fat-shattering dimension. The analysis throws new light on why the SV machine gives good generalization and can also be applied to help explain the performance of the ada-boost algorithm. Some new algorithmic strategies suggested by the perspective will be discussed. General Cost Functions for Support Vector RegressionAlex Smola, GMD Berlin The concept of Support Vector Regression is extended to a more general class of convex cost functions. Moreover it is shown how the resulting convex constrained optimization problems can be efficiently solved by a Primal–Dual Interior Point path following method. Both computational feasibility and improvement of estimation is demonstrated in the experiments. Support Vector ANOVA DecompositionMark O. Stitson, Royal Holloway London This talk will introduce Support Vector ANOVA decomposition (SVAD) applied to a well known data set. SVAD is used with various kernels and preliminary results have shown that SVAD performs better than the respective non ANOVA decomposition kernels. The Boston housing data set from UCI has been tested on Bagging and Support Vector methods before (Drucker et. al.) and these results are compared to the SVAD method. Comparisons on different parameter selections for SVAD are also given and the open question of ideal parameter selection is posed. The SVM method of function approximationV. Vapnik, AT&T Research This talk will address the representation of high dimensional functions using Support Vector Machines. Besides being a learning algorithm, Support Vector Machines provide a linear and compact representation of high dimensional non linear functions. These properties (compacity and linearity) provide several opportunities which I would like to discuss. Reproducing Kernel Hilbert Spaces, Smoothing Spline ANOVA spaces, Support Vector Machines, and all that.Grace Wahba, Statistics, University of Wisconsin-Madison In this (mostly) review talk, We look at reproducing kernel Hilbert spaces (rkhs) as a natural home for studying certain support vector machines and their relations with other multivariate function estimation paradigms. We examine Lemma 6.1 of Kimeldorf and Wahba (J. Math. Anal. Applic. 1971, p 92) concerning linear inequality constraints in rkhs, and note how it applies in arbitrary rkhs. We will particularly note the potential use of the reproducing kernels (rk's) associated with smoothing spline ANOVA spaces, for applications with heterogenous predictor variables, and possibly as a tool in variable selection as well as exemplar selection. Questions about the possible internal ‘tuning’ of SVM's (as compared to the use of test sets) and the ‘degrees of freedom for signal’ will be raised, although probably not answered. Density Estimation using Support Vector MachinesJason Weston, Royal Holloway London I show how the SV technique of solving linear operator equations can be applied to the problem of density estimation. I describe a new optimisation procedure and set of kernels closely related to current SV techniques that guarantee the monotonicity of the approximation. This technique estimates densities with a mixture of bumps (Gaussian-like shapes), with the usual SV property that only some coefficients are non-zero. Both the width and the height of each bump is chosen adaptively, by considering a dictionary of several kernel functions. There is empirical evidence that the regularization parameter gives good control of the approximation, and that the choice of this parameter is universal with respect to the number of sample points, and can even be fixed with good results. back |
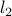 norm to measure the length of the vector that defines the linear separator and the length of the “largest” example. On the other hand, in adaboost, the separation vector is measured using the
norm to measure the length of the vector that defines the linear separator and the length of the “largest” example. On the other hand, in adaboost, the separation vector is measured using the 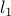 norm and the examples are measured using the
norm and the examples are measured using the 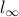 norm (max norm). This technical difference is the reason that adaboost is closely related to linear programming while SVM is related to quadratic programming. It also results in incomparable theoretical performance bounds.
norm (max norm). This technical difference is the reason that adaboost is closely related to linear programming while SVM is related to quadratic programming. It also results in incomparable theoretical performance bounds.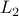 distance of their weight vectors, but by their disagreement distance on the natural distribution of unlabeled examples. I show that this simple trick can lead to significant improvements in generalization accuracy in several simulated domains. (More thorough empirical studies are ongoing.)
I also show how this generalizes the basic maximum margin idea: by measuring hypothesis distances in terms of intrinsic disagreement distance, we can now apply the basic maximum margin idea to arbitrary concept classes, like decision lists and decision trees (provided one can surmount the associated computational barriers).
distance of their weight vectors, but by their disagreement distance on the natural distribution of unlabeled examples. I show that this simple trick can lead to significant improvements in generalization accuracy in several simulated domains. (More thorough empirical studies are ongoing.)
I also show how this generalizes the basic maximum margin idea: by measuring hypothesis distances in terms of intrinsic disagreement distance, we can now apply the basic maximum margin idea to arbitrary concept classes, like decision lists and decision trees (provided one can surmount the associated computational barriers).