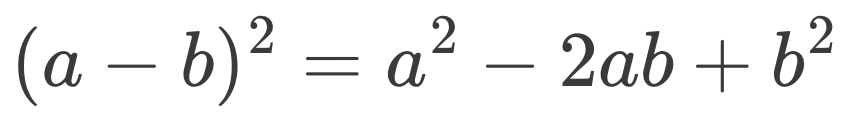
Here’s a simple trick you can use to compute pairs of distances: use the second binomial formula and a linear algebra library. These problems occur in RBF kernel computations (this is how it was implemented e.g. in the Elefant library) and in k-nearest neighbor and EM clustering algorithms. It’s also used for distance-based activations and there are entire libraries for efficient nearest neighbor retrieval, such as FAISS and NMSLib.
The problem: given sets \(X = \{x_1, \ldots, x_n\} \subset \mathbb{R}^d\) and \(Z = \{z_1, \ldots, z_m\} \subset \mathbb{R}^d\) compute the matrix of pairwise squared distances.
\[D \in \mathbb{R}^{n \times m} \text{ where } D_{ij} = \|x_i - z_j\|^2\]
A simple solution is to use a double for loop, take differences, square them and be happy. This is slow for a number of reasons: it isn’t optimized for the architecture (CPUs and GPUs love matrices), it requires you to take differences (an extra operation), and it also means that you aren’t using memory blocking for it (compute is way faster than memory bandwidth). Plus it’d be quite some work to write a multithreaded code for it.
A much faster and simpler solution is to use the second binomial formula to decompose the distance into norms of vectors in \(X\) and \(Z\) and an inner product between them.
\[D_{ij} = \|x_i\|^2 + \|z_j\|^2 - 2 x_i^\top z_j \text{ and hence } D = \bar{x} \cdot 1^\top + 1 \cdot \bar{z}^\top - 2 X^\top Z\]
Here \(\bar{x} \in \mathbb{R}^n\) is given by \(\bar{x}_i = \|x_i\|^2\) and likewise \(\bar{z}\) by \(\bar{z}_j = \|z_j\|^2\). These terms can be computed quickly through row-wise norms in \(O(n d)\) and \(O(m d)\) time respectively. To compute the dot product, simply use matrix-matrix multiplication. This way you get pairwise distance matrices at essentially the same cost as dot products.
For sparse matrices you could be more clever and use an inverted index (Jon Baxter suggested this), or you could be lazy and simply let a sparse matrix linear algebra library to do the work for you.