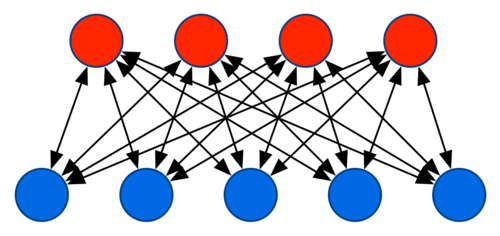
One of the key features of a parameter server is that it, well, serves parameters. In particular, it serves more parameters than a single machine can typically hold and provides more bandwidth than what a single machine offers. A sensible strategy to increase both aspects is to arrange data in the form of a bipartite graph with clients on one side and the server machines on the other. This way bandwidth and storage increase linearly with the number of machines involved. This is well understood. For instance, distributed (key,value) stores such as memcached or Basho Riak use it. It dates back to the ideas put forward by David Karger et al. on Consistent Hashing and Random Trees in STOC 1997.
A key problem is that we can obviously not store a mapping table from the keys to the machines. This would require a database that is of the same size as the set of keys and that would need to be maintained and updated on each client. One way around this is to use the argmin hash mapping. That is, given a machine pool \(M\), we assign a given (key,value) pair to the machine that has the smallest hash, i.e.
\[m(k,M)=\mathop{\mathrm{argmin}}_{m \in M}(m,k)\]
The advantage of this scheme is that it allows for really good load balancing and repair. First off, the load is almost uniformly distributed, short of a small number of heavy hitters. Secondly, if a machine is removed or added to the machine pool, rebalancing affects all other machines uniformly. To see this, notice that the choice of machine with the smallest and second-smallest hash value is uniform.
Unfortunately, this is a stupid way of distributing (key,value) pairs for machine learning. And this is what we did in our 2010’ VLDB and 2012’ WSDM papers. To our excuse, we didn’t know any better. And others copied that approach … after all, how you can you improve on such nice rebalancing aspects.
This begs the question why it is a bad idea. It all comes down to the issue of synchronization. Basically, whenever a client attempts to synchronize its keys, it needs to traverse the list of the keys it owns and communicate with the appropriate servers. In the above scheme, it means that we need to communicate to a new random server for each key. This is amazingly costly. Probably the best comparison would be a P2P network where each byte is owned by a different machine. Downloads would take forever.
We ‘fixed’ this problem by cleverly reordering the access and then performing a few other steps of randomization. There’s even a nice load balancing lemma in the 2012 WSDM paper. However, a much better solution is to prevent the problem from happening and to borrow from key distribution algorithms such as Chord. In it, servers are inserted into a ring via a hash function. So are keys. This means that each server now owns a contiguous segment of keys. As a result, we can easily determine which keys go to which server, simply by knowing where in the ring the server sits.
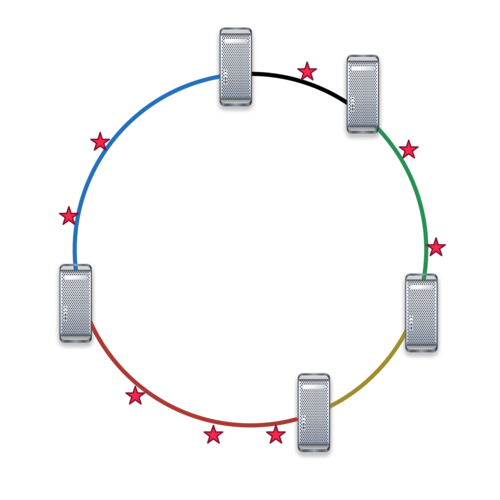
In the picture above, keys are represented by little red stars. They are randomly assigned using a hash function via h(k) to the segments ‘owned’ by servers s that are inserted in the same way, i.e. via h(s). In the picture above, each server ‘owns’ the segment to its left. Also have a look at the Amazon Dynamo paper by DeCandia et al., 2007 SOSP for a related description.
Obviously, such a load-balancing isn’t quite as ideal as the argmin hash. For instance, if a machine fails, the next machine inherits the entire segment. However, by inserting each server logn times we can ensure that a good load balance is achieved and also that when machines are removed, there are several other machines that pick up the work. Moreover, it is now also very easy to replicate things (more on this later). If you’re curious on how to do this, have a look at Amar Phanishayee’s excellent thesis. In a nutshell, the machines to the left hold the replicas.