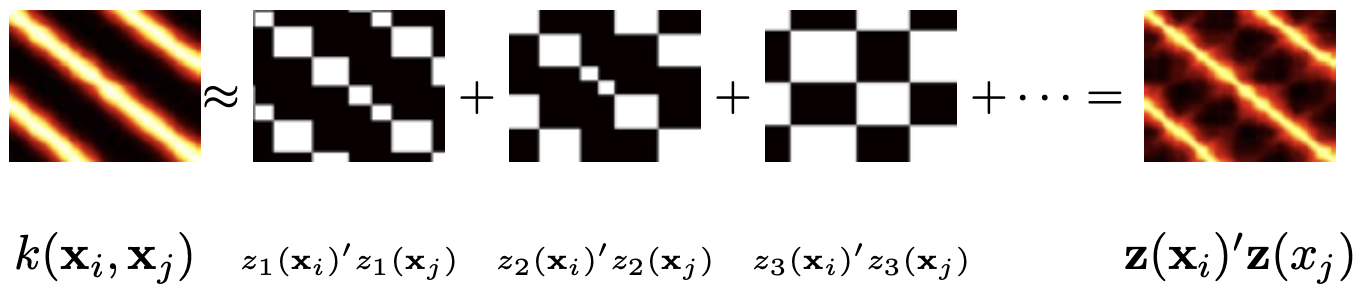
So you read a book on Reproducing Kernel Hilbert Spaces and you’d like to try out this kernel thing. But you’ve got a lot of data and most algorithms will give you an expansion that requires a number of kernel functions linear in the amount of data. Not good if you’ve got millions to billions of instances.
You could try out low rank expansions such as the Nystrom method of Seeger and Williams, 2000, the randomized Sparse Greedy Matrix Approximation of Smola and Schölkopf, 2000 (the Nyström method is a special case where we only randomize by a single term), or the very efficient positive diagonal pivoting trick of Scheinberg and Fine, 2001. Alas, all those methods suffer from a serious problem: at training you need to multiply by the inverse of the reduced covariance matrix, which is \(O(d^2)\) cost for a \(d\) dimensional expansion. An example of an online algorithm that suffers from the same problem is this (NIPS award winning) paper of Csato and Opper, 2002. Assuming that we’d like to have d grow with the sample size this is not a very useful strategy. Instead, we want to find a method which has \(O(d)\) cost for \(d\) attributes yet shares good regularization properties that can be properly analyzed.
Enter Radford Neal’s seminal paper from 1994 on Gaussian Processes (a famous NIPS reject). In it he shows that a Neural Network with an infinite number of nodes and a Gaussian Prior over coefficients converges to a GP. More specifically, we get the kernel
\[k(x,x′)=\mathbb{E}_c [\phi_c(x) \phi_c(x′)]\]
Here \(\phi_c(x)\) is a function parametrized by \(c\), e.g. the location of a basis function, the degree of a polynomial, or the direction of a Fourier basis function. There is also a discussion regarding RKHS in a paper by Smola, Schölkof and Müller, 1998 that discusses this phenomenon in regularization networks. These ideas were promptly forgotten by its authors. One exception is the empirical kernel map where one uses a generic design matrix that is generated through the observations directly.
It was not until the paper by Rahimi and Recht, 2008 on random kitchen sinks that this idea regained popularity. In a nutshell the algorithm works as follows: Draw \(d\) values \(c_i\) from the distribution over \(c\). Use the corresponding basis functions in a linear model with quadratic penalty on the expansion coefficients. This method works whenever the basis functions are well bounded. For instance, for the Fourier basis the functions are bounded by \(1\). The proof of convergence of the explicit function expansion to the kernel is then a simple consequence of Chernoff bounds.
In the random kitchen sinks paper Rahimi and Recht discuss RBF kernels and binary indicator functions. However, this works more generally for any set of well behaved set of basis functions used in generating a random design matrix. A few examples:
- Fourier basis with Gaussian parameters. Take functions of the form \(e^{i \omega^\top x}\) where the coefficients \(\omega\) are drawn from a Gaussian. This is the random kitchen sinks paper. Obviously you can use hash functions rather than an actual random number generator. This ensures that you don’t need to store all parameters \(\omega\).
- Pick random separating hyperplanes. This will effectively give you functions of bounded variation. Use the empirical kernel map, i.e. we use some function \(k(x,x')\) for which we employ for \(x'\) a random subset of the data we wish to train on.
- Pick suitable binary features obtained via binning (the figure on top, taken from Rahimi and Recht, 2008, shows quite impressive results in lower dimensions).