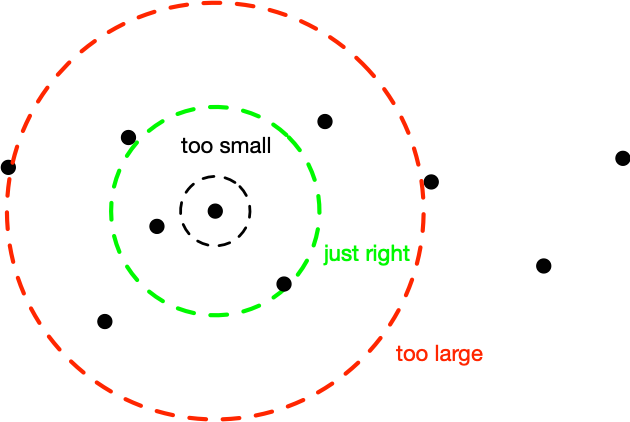
This is an idea that was originally put forward by Bernhard Schölkopf in his thesis: Assume you have an RBF (radial basis function) kernel and you want to know how to scale it. Recall that such a kernel is given by
\[k(x,x') = \kappa(\lambda \|x - x'\|)\]
For instance, Gaussian RBFs can be written as \(k(x,x') = \exp(-\lambda^2 \|x-x'\|^2)\). We want that the argument of this function is \(O(1)\) for typical pairs of instances \(x\) and \(x’\). Bernhard proposed to look at the dimensionality of x and rescale accordingly. This is a great heuristic. But it ignores correlation between the coordinates. A much simpler trick is to pick, say 1000 pairs \((x,x’)\) at random from your dataset, compute the distance of all such pairs and take the median, the \(0.1\) and the \(0.9\) quantile. Now pick \(\lambda\) to be the inverse any of these three numbers. With a little bit of crossvalidation you will figure out which one of the three is best. In most cases you won’t need to search any further.