Bloom filters are one of the really ingenious and simple building blocks for randomized data structures. A great summary is the paper by Broder and Mitzenmacher, 2005. The figure above is from their paper. In this post I will briefly review its key ideas since it forms the basis of the Count-Min sketch of Cormode and Muthukrishnan, 2003 it will also be necessary for an accelerated version of the graph kernel of Shervashidze et al., 2011, and finally, a similar structure will be needed to compute data streams over time for a real-time sketching service.
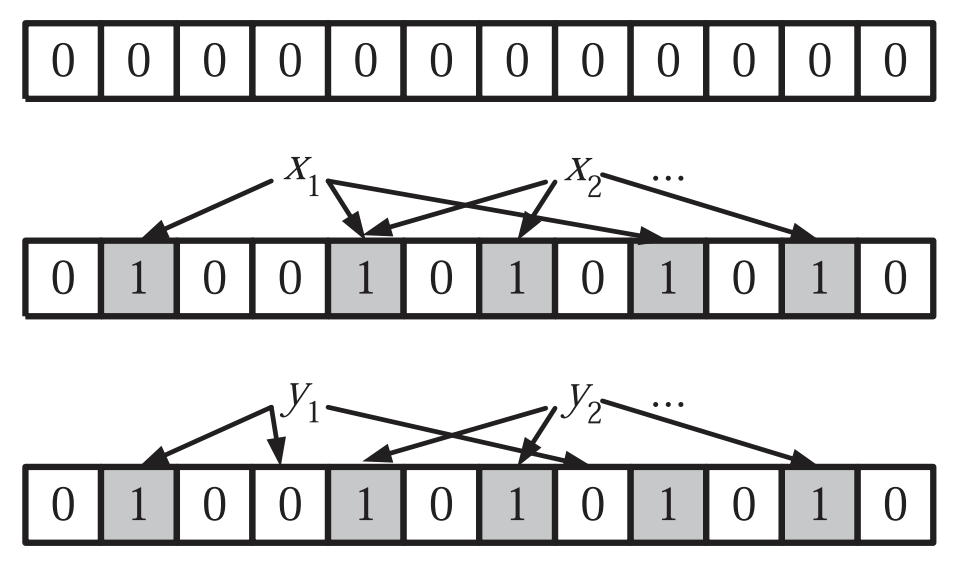
At its heart a Bloom filter uses a bit vector of length \(N\) and a set of \(k\) hash functions mapping arbitrary keys \(x\) into their hash values \(h_i(x) \in \{0, \ldots N-1\}\) where \(i \in \{0, \ldots k-1\}\) denotes the hash function. The Bloom filter allows us to perform approximate set membership tests where we have no false negatives but we may have a small number of false positives.
- Initialize(b)
Set all \(b[i]=0\) - Insert(b,x)
For all \(i \in \{0, \ldots k\}\) set \(b[h_i(x)]=1\) - Query(b, x)
Return true if \(b[h_i(x)]=1\) for all \(i \in \{0, \ldots \}\). Return false otherwise.
Furthermore, unions and intersections between sets are easily achieved by performing bit-wise OR and AND operations on the bloom hashes of the corresponding sets respectively. Since these are bit-wise operations, they can be very fast, essentially operating at memory speed.
It is clear that if we inserted \(x\) into the Bloom filter the query will return true, since all relevant bits in \(b\) are set to \(1\). But we could get unlucky. To analyze the probability of a false positive take the probability of a bit being 1. After inserting \(m\) items using \(k\) hash functions over a range of \(N\) we have
\[\Pr(b[i]=1) = 1−\left(1−\frac{1}{N}\right)^{km} \approx 1−\exp\left(−\frac{km}{N}\right)\]
For a false positive to occur we need to have all k bits associated with the hash functions to be 1. Ignoring the fact that the hash functions might collide, i.e. \(h_i(x) = h_j(x)\) for some \(i \neq j\), the probability of false positives is given by
\[p \approx \left(1−\exp\left(−\frac{km}{N}\right)\right)^k\]
Taking derivatives with respect to \(\frac{km}{N}\) shows that the minimum is obtained for \(\log 2\), that is \(k =\frac{N}{m} \log 2\). In other words, \(k\) decreases with the fill rate \(\frac{N}{m}\) of the Bloom filter. This makes sense since a higher fill rate leads to a higher collision probability and we shouldn’t try to ‘overfill’ the filter. Plugging the optimal value back into \(p\) yields \(p \approx 2^{-k}\), i.e. the quality of the array decreases exponentially with the fill rate, albeit slowly at rate \(\exp(-\frac{N}{m} \log^2 2)\).
One of the really nice properties of the Bloom filter is that all memory is used to store the information about the set rather than an index structure storing the keys of the items. The downside is that it is impossible to read out \(b\) without knowing the queries. Also note that it is impossible to remove items from the Bloom filter once they’ve been inserted. After all, we do not know whether some of the bits might have collided with another key, hence setting the corresponding bits to 0 would cause false negatives.