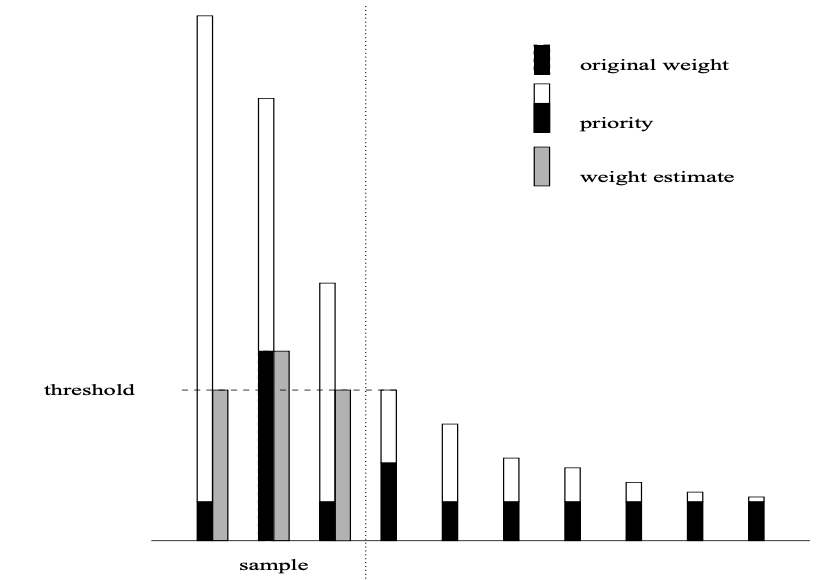
Tamas Sarlos pointed out a much smarter strategy on how to obtain a sparse representation of a (possibly dense) vector: Priority Sampling by Duffield, Lund and Thorup, 2006. The idea is quite ingenious and (surprisingly so) essentially optimal, as Mario Szegedy showed. Here’s the algorithm (please read the previous blog on vector sparsification for some motivation):
- For each \(x_i\) compute a priority \(\pi_i= \frac{x_i}{a_i}\) where \(a_i \sim U(0,1]\) is drawn from a uniform distribution.
- Let \(\tau\) be the \(k+1\) largest such priority.
- Pick all \(k\) indices \(i_1, \ldots i_k\) which satisfy \(\pi_i > \tau\) and assign them the value \(s_i= \mathop{\mathrm{max}}(x_i,\tau)\).
- Set all other coordinates \(s_i\) to \(0\).
This provides an estimator with the following properties:
- The variance is no larger than that of the best \(k+1\)-sparse estimator.
- The entries \(s_i\) satisfy \(\mathbb{E}[s_i]=x_i\), i.e. the expectation is preserved.
- The covariance vanishes, i.e. \(\mathbb{E}[s_i s_j]= x_i x_j\).
Note that we assumed that all \(x_i \geq 0\). If not, simply apply the same algorithm to \(|x_i|\) and return signed versions of the estimate.