After a few discussions within Yahoo I’ve decided to post a bunch of tricks here. A lot of these are well known. Some others might be new. They’re small hacks, too small to put into a paper on their own, unless we allow 1 page papers. But they can make a big difference to make your code go fast or do useful things. So here it goes:
Assume you want to train a model, parametrized by \(w\) to minimize the objective
\[L(w) = \sum_{i=1}^n l_i(w) + \frac{\lambda}{2}\|w^2\|\]
In this case you could perform stochastic gradient updates of the form
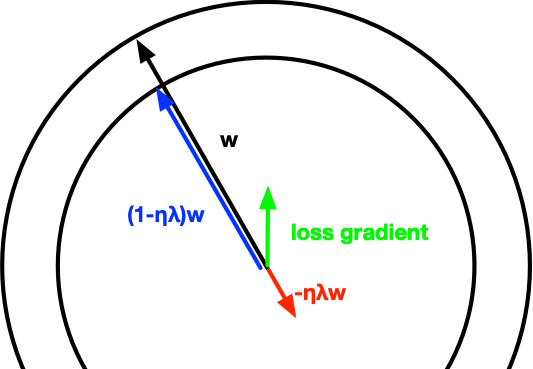
\[w \leftarrow w - \eta \left(\partial_w l_i(w) + \lambda w\right) = (1 - \eta \lambda) w - \eta \partial_w l_i(w)\]
The problem here is that if the gradients are sparse, say 1000 features for a document while \(w\) may have millions, maybe even billions of nonzero coefficients, this update is extremely slow: for each meaningful coefficient update we also update many more coefficients (up to billions) that just shrink summarily. An easy fix is to keep a coefficient, say \(c \in \mathbb{R}\), which tracks the scale separately via \(w = c \bar{w}\). This yields:
\[\begin{aligned}c \bar{w} \leftarrow & (1 - \eta \lambda) c \bar{w} - \eta \partial_{\bar{w}} l_i(c \bar{w}) \\ = & \underbrace{(1 - \eta \lambda)c}_{\mathrm{scalar~update}} \left(\bar{w} - \frac{\eta}{1 - \eta \lambda c} \partial_{\bar{w}} l_i(c \bar{w}) \right) \end{aligned}\]
In other words, we update the scaling coefficient \(c \leftarrow (1 - \eta \lambda)c\) and perform only sparse updates on \(w\). As far as I recall this trick can be found e.g. in Leon Bottou’s stochastic gradient solver, or in Shai Shalev-Schwartz’s Pegasos package. We also used this in the implementation of Kivinen, Williamson & Smola, 1998 on stochastic gradient descent for kernels.